As technology continues to advance, the need for faster and more efficient communication becomes increasingly important. Bandwidth, the range of frequencies that can be transmitted over a communication channel, is a crucial factor in determining the speed and quality of data transmission. However, finding the exact bandwidth of a communication channel can be quite challenging, especially when dealing with complex signals. Fortunately, bode plots offer a simple and effective method for determining the bandwidth of a signal.
A bode plot is a graphical representation of the frequency response of a signal or system. It shows how the signal’s amplitude and phase change with frequency. By analyzing the slope of the bode plot, it is possible to determine the bandwidth of a signal. In this article, we will explore how to use bode plots to find the bandwidth of a signal, step by step, so that you can optimize your communication channels and achieve faster and more efficient data transmission.
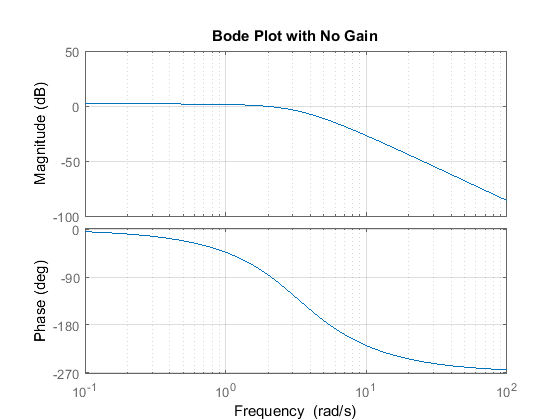
To find the bandwidth from a Bode plot, first plot the graph with the frequency and gain on the vertical and horizontal axes respectively. Look for the frequency at which the gain is equal to -3dB, which is the 3dB bandwidth. This is the frequency at which the magnitude of the transfer function of the circuit is half of the maximum magnitude.
- Plot the graph with the frequency and gain on the vertical and horizontal axes respectively.
- Look for the frequency at which the gain is equal to -3dB.
- This is the frequency at which the magnitude of the transfer function of the circuit is half of the maximum magnitude.
What is a Bode Plot?
A Bode plot is a graphical representation of a system’s transfer function, which is a mathematical representation of the relationship between its input and output. It is useful for understanding the behavior of a system over a range of frequencies. In electrical engineering, the Bode plot is often used to analyze the frequency response of filters, amplifiers, oscillators, and other components.
A Bode plot consists of two curves, one for the magnitude of the response and one for the phase of the response. Each curve is plotted against frequency, with the horizontal axis representing frequency, and the vertical axis representing the magnitude and phase. With this plot, it is possible to understand how the system will respond to different frequencies.
How to Find Bandwidth from a Bode Plot
The bandwidth of a system is the range of frequencies over which it is capable of responding. In a Bode plot, the bandwidth of a system is represented by the points at which the magnitude curve crosses the 0dB line. This is known as the -3dB bandwidth, as the response of the system is attenuated by 3dB at this point.
To find the bandwidth of a system from a Bode plot, simply find the two points on the magnitude curve where it crosses the 0dB line. The difference between these two points is the 3dB bandwidth. This is the range of frequencies over which the system will respond to input.
Calculating the Bandwidth of a System
Once the -3dB bandwidth of a system has been determined from a Bode plot, it is possible to calculate the bandwidth of the system more accurately. This can be done by finding the points on the magnitude curve where the response has been attenuated by a certain amount, such as 6dB or 10dB. The difference between these two points is the bandwidth of the system.
It is also possible to calculate the bandwidth of a system by taking the ratio of the highest and lowest frequencies of the system. This is known as the 3dB bandwidth ratio, and is calculated by taking the ratio of the -3dB bandwidth and the system’s center frequency. This can be used to estimate the bandwidth of a system without plotting the Bode plot.
Using the Bode Plot to Analyze a System
In addition to finding the bandwidth of a system from a Bode plot, the plot can also be used to analyze the behavior of a system at different frequencies. The magnitude curve can be used to determine the gain of the system at different frequencies, and the phase curve can be used to determine the phase shift of the system at different frequencies.
By analyzing the behavior of a system at different frequencies, it is possible to gain insight into the performance of the system and check whether it meets the desired specifications. The Bode plot is a powerful tool for understanding the behavior of a system and can be used to design better systems.
Frequently Asked Questions
How to find bandwidth from bode plot?
What is a Bode Plot?
A Bode plot is a graph that plots the magnitude and phase of a transfer function for a given frequency. It is used to visualize and analyze the frequency response of a transfer function. The magnitude plot shows the ratio of the output to the input, while the phase plot shows the time delay between the output and input.
How do I find the bandwidth from a Bode Plot?
The bandwidth of a transfer function can be determined by finding the frequency of the 3 dB point, or the point at which the magnitude of the transfer function is -3 dB. This frequency is the bandwidth and is commonly referred to as the -3 dB bandwidth. To find this frequency, locate the -3 dB point on the magnitude plot and then find the corresponding frequency. This frequency is the bandwidth of the transfer function.
What is the -3 dB Bandwidth?
The -3 dB bandwidth is the frequency at which the magnitude of the transfer function is -3 dB. This frequency is usually used to measure the bandwidth of a transfer function and is commonly referred to as the -3 dB bandwidth. It is important to remember that the -3 dB bandwidth does not indicate the frequency range of the transfer function; it only indicates the frequency at which the magnitude is -3 dB.
What is the meaning of -3 dB?
The term -3 dB is used to describe the magnitude of a transfer function at a certain frequency. It is the point at which the magnitude of the transfer function is -3 dB, or half the maximum magnitude. This point is commonly used to measure the bandwidth of a transfer function.
How can I use a Bode Plot to determine the stability of a system?
A Bode plot can be used to determine the stability of a system. The phase plot of the Bode plot shows the time delay between the output and input of the system. If the phase plot is flat and the magnitude plot is positive, then the system is stable. If the phase plot is not flat and the magnitude plot is negative, then the system is unstable. By looking at the magnitude and phase plots, you can determine if the system is stable or not.
Bode diagrams 18 – bandwidth
In conclusion, understanding how to find bandwidth from a Bode plot is a valuable skill for any engineer or scientist working in the field of signal processing. The ability to accurately analyze and interpret Bode plots can help to identify the critical frequency components of a signal, and ultimately improve the performance of a system. By understanding the key features of a Bode plot, such as the gain and phase margins, and the location of the poles and zeros, one can quickly and easily determine the bandwidth of a system.
In today’s fast-paced world where technology is advancing rapidly, having a strong grasp of signal processing concepts is becoming increasingly important. Whether you are working in telecommunications, audio engineering, or any other field that relies on signal processing, being able to analyze and interpret Bode plots can give you a critical edge in your work. By following the guidelines outlined in this article, you can confidently find the bandwidth of any system from its Bode plot and take your signal processing skills to the next level.