Quantum mechanics is a fascinating field of physics that deals with the behavior of particles on a microscopic level. It is a complex subject that can be quite intimidating, especially for those who are new to the field. One of the key concepts in quantum mechanics is the expectation value, which is a measure of the average outcome of a measurement of a particular property of a particle.
The expectation value is a crucial tool in quantum mechanics as it allows scientists to predict the behavior of particles in different situations. In this article, we will explore what the expectation value is, how to calculate it, and how it is used in quantum mechanics. Whether you are a student of physics or simply interested in learning more about this fascinating subject, this article will provide you with a comprehensive guide to finding the expectation value in quantum mechanics.
Expectation value in quantum mechanics can be found by following these steps:
- Calculate the wavefunction of the system.
- Determine the Hamiltonian operator.
- Calculate the matrix elements of the Hamiltonian operator.
- Calculate the expectation value of the Hamiltonian operator.
The expectation value of the Hamiltonian operator is an important quantity in quantum mechanics and is used to calculate properties such as energy levels, transition rates and more.

What is Expectation Value in Quantum Mechanics?
Expectation value in quantum mechanics is the average value of a physical quantity when it is measured over a large number of trials. It is calculated by multiplying the probability of each possible result by the value of the result and then summing the products. This value is a useful tool for understanding the behavior of a quantum system.
How to Find Expectation Value in Quantum Mechanics?
Step 1: Determine the Physical Quantity
The first step to finding the expectation value of a physical quantity in quantum mechanics is to determine the physical quantity that is being measured. This may be anything from the position of a particle to its momentum or energy. Once the physical quantity is determined, the next step is to calculate the probability of each possible outcome.
Step 2: Calculate the Probability of Each Outcome
The next step is to calculate the probability of each outcome. This can be done by using the wave function of the quantum system. The wave function gives the probability of finding a particle in each state. The probability of each outcome is then determined by multiplying the wave function by its conjugate, and then summing the product over all possible states.
Step 3: Calculate the Expectation Value
Once the probability of each outcome is calculated, the expectation value can be determined. This is done by multiplying the probability of each outcome by the value of that outcome and then summing the products. This gives the expectation value for the physical quantity being measured.
Step 4: Calculate the Uncertainty
The uncertainty in the expectation value can also be determined. This is done by calculating the variance of the probability distribution. The variance is the sum of the squared differences between the probability of each outcome and the expectation value, divided by the number of trials.
Step 5: Analyze the Results
Once the expectation value and the uncertainty are calculated, the results can be analyzed. This can be done by plotting the probability distribution, which gives an idea of how the physical quantity is distributed in the system. The expectation value and the uncertainty can then be compared to the theoretical values to determine how accurately the quantum system is behaving.
Frequently Asked Questions about How to Find Expectation Value in Quantum Mechanics
Here you will find answers to some of the most commonly asked questions about how to find expectation value in quantum mechanics. We will discuss how to calculate expectation values, how to find the expectation value of a single particle, and how to find the expectation value of two particles.
What is an Expectation Value?
An expectation value is a mathematical representation of the average value of a physical quantity. It is used to describe the average behavior of a system and is calculated by taking the expectation value of the physical quantity, divided by the total number of measurements. Expectation values are also useful for predicting the outcome of measurements.
How Do You Calculate Expectation Values?
To calculate the expectation value of a physical quantity, you must first define the Hamiltonian of the system, which describes the energy of the system. Once the Hamiltonian is defined, the expectation value of the physical quantity can be calculated by taking the expectation value of the Hamiltonian times the physical quantity, divided by the total number of measurements.
How Do You Find the Expectation Value of a Single Particle?
To find the expectation value of a single particle, you must first calculate the wavefunction of the particle. This can be done by solving the Schrödinger equation using the Hamiltonian of the system. Once the wavefunction is known, the expectation value of the particle can be found by taking the expectation value of the wavefunction times the physical quantity, divided by the total number of measurements.
How Do You Find the Expectation Value of Two Particles?
To find the expectation value of two particles, you must first calculate the wavefunction of the particles. This can be done by solving the two-particle Schrödinger equation using the Hamiltonian of the system. Once the wavefunction is known, the expectation value of the two particles can be found by taking the expectation value of the wavefunction times the physical quantity, divided by the total number of measurements.
What Is the Difference Between the Expectation Value and the Mean Value?
The expectation value is a mathematical representation of the average value of a physical quantity, while the mean value is the average of the values measured in a set of measurements. The expectation value is calculated using the expectation value of the physical quantity, while the mean value is calculated using the average value of the measurements. The expectation value is more accurate than the mean value, as it takes into account the probability of the physical quantity occurring.
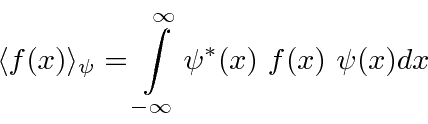
Expectation value
In conclusion, finding the expectation value in quantum mechanics requires a deep understanding of the mathematical principles and concepts involved. However, with the right tools and knowledge, it is possible to calculate the expectation value of any quantum mechanical system accurately. The expectation value is a crucial tool in understanding the behavior of quantum systems and is used in many applications, including quantum computing and quantum cryptography.
As we continue to explore the fascinating world of quantum mechanics, we must keep in mind that it is a complex and intricate field that requires patience, dedication, and a deep understanding of mathematics. By learning how to find the expectation value, we are one step closer to unlocking the mysteries of the quantum universe and harnessing its power for the betterment of mankind. With continued research and development, we can expect to see even more groundbreaking discoveries in the field of quantum mechanics in the years to come.