Are Are Quantum Gates Unitary?

Quantum computing is a fascinating field that has captured the attention of scientists and researchers from all over the world. It has the potential to revolutionize the way we approach problems that are too complex for classical computers to solve. One of the fundamental concepts that underpins quantum computing is the idea of quantum gates. These gates are the building blocks of quantum circuits, and they enable us to manipulate qubits – the basic units of quantum information. However, there is a question that often arises when discussing quantum gates: are they unitary?

Unitarity is a crucial property of quantum mechanics that ensures the conservation of probability. In other words, the total probability of all possible outcomes of a quantum system must add up to one. Unitary operations are those that preserve this property – they transform a quantum state into another quantum state while maintaining the probabilities of all possible outcomes. So, are quantum gates unitary? The answer is not straightforward, and it requires us to delve deeper into the nature of quantum gates and their mathematical representations. In this article, we will explore what it means for a quantum gate to be unitary and why it matters in the context of quantum computing.

Are Quantum Gates Unitary?

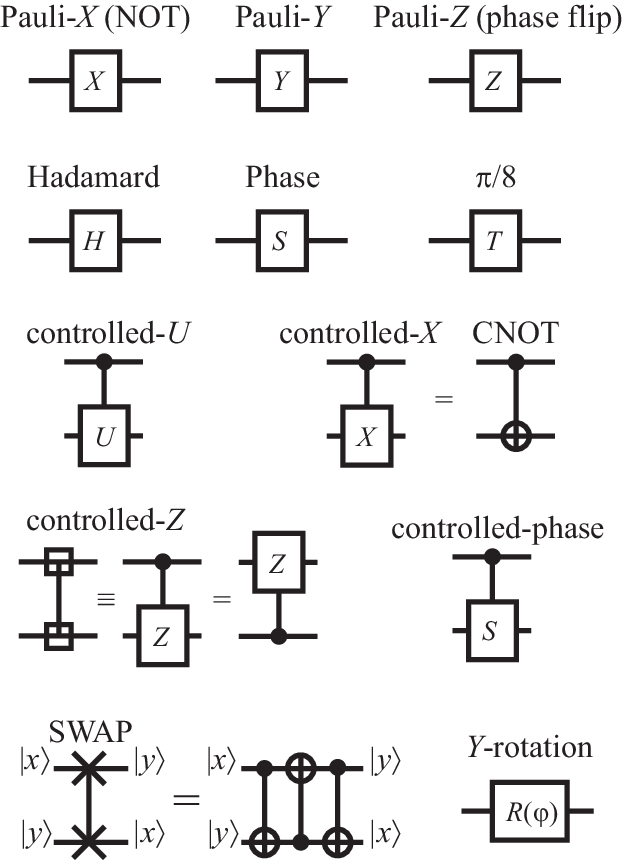
Quantum gates are a type of quantum logic gate used in quantum computing. They are used to manipulate qubits, the basic unit of quantum information. Quantum gates can be used to perform quantum operations on qubits, which can be used to solve complex problems that would otherwise be difficult to solve classically. Quantum gates are unitary, meaning they can be used to construct a unitary transformation, which is an operation that preserves the state of the qubits.

What is a Quantum Gate?

A quantum gate is a device used in quantum computing to manipulate qubits. It is analogous to a classical logic gate, but it acts on qubits instead of classical bits. Quantum gates can be used to perform operations on qubits, such as entanglement, rotation, and measurement. These operations are essential for quantum computing and can be used to solve complex problems.

Quantum gates can be represented by matrices, which are used to describe the transformation of qubits. These matrices are unitary, meaning that they can be used to construct a unitary transformation, which is an operation that preserves the state of the qubits. This is an essential property for quantum computing, as it allows for the manipulation of qubits with precision.

How Do Quantum Gates Work?

Quantum gates are used to manipulate the state of qubits. They can be represented by unitary matrices, which are used to describe the transformation of qubits. Quantum gates can be used to perform operations on qubits, such as entanglement, rotation, and measurement. These operations are essential for quantum computing and can be used to solve complex problems.

Quantum gates work by altering the state of qubits using unitary matrices. These matrices can be used to construct a unitary transformation, which is an operation that preserves the state of the qubits. This is an essential property for quantum computing, as it allows for the manipulation of qubits with precision.

What Are the Benefits of Using Quantum Gates?

Quantum gates are an essential component of quantum computing. They are used to manipulate the state of qubits and can be used to perform operations on qubits, such as entanglement, rotation, and measurement. These operations are essential for quantum computing and can be used to solve complex problems.

The use of quantum gates also has several advantages over classical computing. Quantum gates are faster and more efficient than classical gates, as they can be used to perform operations on qubits in parallel. They also have the advantage of being unitary, meaning that they can be used to construct a unitary transformation, which is an operation that preserves the state of the qubits. This is an essential property for quantum computing, as it allows for the manipulation of qubits with precision.

Are Quantum Gates Unitary?

Yes, quantum gates are unitary. This means that they can be used to construct a unitary transformation, which is an operation that preserves the state of the qubits. This is an essential property for quantum computing, as it allows for the manipulation of qubits with precision.

Quantum gates are represented by unitary matrices, which are used to describe the transformation of qubits. These matrices can be used to construct a unitary transformation, which is an operation that preserves the state of the qubits. This is an essential property for quantum computing, as it allows for the manipulation of qubits with precision.

Frequently Asked Questions

Quantum gates are the building blocks of quantum computers. In this article, we will answer some of the most common questions about quantum gates and how they work.

What are quantum gates?

Quantum gates are the basic operations of quantum computing. They are unitary transformations, which means they can be represented as matrices, and they can be used to transform a quantum state from one state to another. Quantum gates are used to create quantum circuits, which are quantum algorithms written as quantum circuits.

Quantum gates can be used to perform a wide range of operations, including quantum logic operations, quantum Fourier transforms, and quantum error correction. They can also be used to perform a variety of different tasks, such as creating entanglement between particles, and performing quantum teleportation.

Are quantum gates unitary?

Yes, quantum gates are unitary. Unitary transformations are transformations which preserve the total energy and the total probability of the system. This means that the system is always in the same state, regardless of how many operations are performed. In quantum computing, unitary gates are used to manipulate qubits, which are the basic elements of a quantum circuit.

Unitary transformations are also reversible, meaning that the output of a quantum gate is the same as the input. This makes them particularly useful for creating quantum algorithms, as they can be used to create complex circuits with a single gate. Unitary gates are often used to create entanglement between qubits, and they can also be used to perform quantum teleportation, which is the transfer of quantum information from one point to another.

What are the different types of quantum gates?

There are a variety of different types of quantum gates, including single-qubit gates, two-qubit gates, and multi-qubit gates. Single-qubit gates are used to manipulate a single qubit, while two-qubit gates are used to manipulate two qubits at the same time. Multi-qubit gates are used to manipulate a larger number of qubits at once.

Single-qubit gates are the most basic type of quantum gate, and they are used to manipulate the state of a single qubit. Two-qubit gates are used to manipulate the state of two qubits, and they are often used to create entanglement between qubits. Multi-qubit gates are used to manipulate a larger number of qubits at once, and they are often used to perform quantum teleportation.

How are quantum gates used?

Quantum gates are used to create quantum algorithms, which are programs written in quantum circuits. Quantum circuits are made up of a series of quantum gates, which can be used to perform a variety of operations. Quantum algorithms are used to solve complex problems that are not solvable with traditional computers, such as factoring large numbers or searching large databases.

Quantum gates can also be used to create entanglement between qubits, and they can be used to perform quantum teleportation. Additionally, quantum gates can be used to perform a variety of operations, such as quantum Fourier transforms, and quantum error correction.

What are the advantages of quantum gates?

Quantum gates have a number of advantages over traditional computing. They are faster and more efficient than traditional computers, as they can perform a variety of operations in a single step. Additionally, quantum gates can be used to create entanglement between qubits, which allows for faster and more accurate calculations.

Finally, quantum gates are reversible, meaning that the output of a quantum gate is the same as the input. This makes them particularly useful for creating complex quantum algorithms, as they can be used to create complex circuits with a single gate. This makes them ideal for solving complex problems that are not solvable with traditional computers.

Ch 11: What are unitary operators? | Maths of Quantum Mechanics

In conclusion, the question of whether quantum gates are unitary is a fundamental one in the field of quantum computing. Unitarity is a necessary condition for the reversibility of quantum gates, which is critical for the accurate manipulation of quantum states. The answer to this question lies in the mathematical representation of quantum gates, which can be seen as transformations on the Hilbert space of quantum states. By definition, unitary operators preserve the inner product of the Hilbert space, and therefore, quantum gates must also be unitary.

The importance of unitarity in quantum computing cannot be overstated. It is the foundation on which the entire field is built, and without it, quantum computation would not be possible. With the development of increasingly complex quantum algorithms, the role of unitarity in the design and implementation of quantum gates will only become more critical. As researchers continue to push the boundaries of what is possible in quantum computing, the question of whether quantum gates are unitary will remain a central topic of inquiry.