Quantum computing has become increasingly popular in recent years due to its potential to revolutionize the way we process information. One of the fundamental building blocks of quantum computing is the quantum gate. A quantum gate is a mathematical operation that acts on a quantum system, allowing us to manipulate the state of the system. However, a question that often arises in the world of quantum computing is whether these gates have to be unitary.
Unitarity is a fundamental property of quantum mechanics, and it is closely related to the conservation of probability. In simple terms, a unitary operation preserves the probability of finding a particle in a particular state. This property is critical in quantum computing because it allows us to ensure that the probability of measuring a specific output state is equal to the probability of measuring the corresponding input state. Therefore, it is natural to ask whether quantum gates must be unitary to ensure that the probabilities are conserved. In this article, we will explore the concept of unitarity in quantum computing and discuss whether quantum gates have to be unitary.

Do Quantum Gates Have to Be Unitary?
Quantum computing has opened a world of possibilities for scientists and researchers, allowing for the development of powerful algorithms that can be used to solve complex problems. One of the most important concepts in quantum computing is the concept of a quantum gate, which is a type of quantum circuit that is used to manipulate the quantum state of a system. The question of whether or not quantum gates have to be unitary has been the source of much debate in the quantum computing community. In this article, we will examine the issue in greater detail.
What is a Quantum Gate?
A quantum gate is a device that can manipulate the quantum state of a system. It is a fundamental component of quantum computing, as it is used to create and manipulate quantum algorithms. In general, quantum gates are comprised of a set of logic gates that are used to control the flow of quantum information. These gates can be used to create different types of quantum algorithms, as well as to manipulate the states of qubits.
Do Quantum Gates Have to Be Unitary?
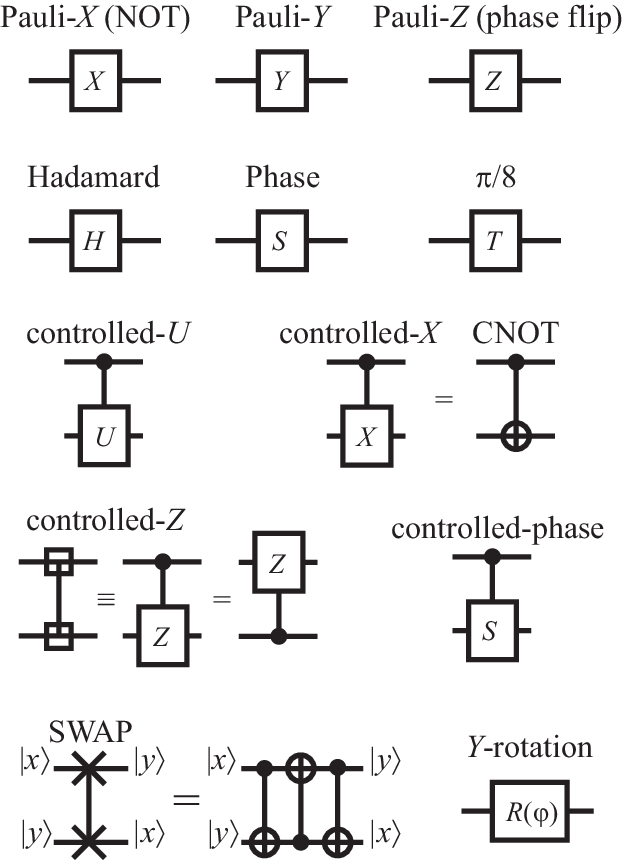
The question of whether or not quantum gates have to be unitary has been the subject of much debate in the quantum computing community. Unitary gates are those which preserve the norm of the quantum state, meaning that the probability of a given state is unchanged. For example, a Hadamard gate is a unitary gate, as it preserves the norm of the quantum state.
On the other hand, non-unitary gates are those which do not preserve the norm of the quantum state. Such gates can be used to create quantum algorithms that are not unitary, as they can be used to manipulate the quantum state in a way that does not preserve the norm. This means that non-unitary gates can be used to create algorithms that are not strictly unitary.
It is important to note, however, that non-unitary gates can also be used to create algorithms that are unitary, as they can be used to manipulate the quantum state in a way that is consistent with the principles of unitarity. Therefore, it is possible to use non-unitary gates to create unitary algorithms.
Benefits of Unitary Gates
Unitary gates are generally considered to be preferable for quantum computing, as they offer several advantages over non-unitary gates. For example, unitary gates are typically more efficient than non-unitary gates, as they require fewer operations to achieve a given result. Additionally, unitary gates generally require less energy to operate, making them more power-efficient.
Furthermore, unitary gates are also better suited for certain types of algorithms, as they can be used to create algorithms that are more stable and reliable. This can be particularly useful for algorithms that require a high degree of reliability, such as those used in cryptography.
Conclusion
In conclusion, quantum gates do not necessarily have to be unitary. Non-unitary gates can be used to create algorithms that are not strictly unitary, but they can also be used to create algorithms that are unitary. Unitary gates are generally considered to be preferable for quantum computing, as they offer a number of advantages over non-unitary gates.
Frequently Asked Questions
Quantum gates are a fundamental part of quantum information processing. They are used to manipulate quantum information in a way that is consistent with the laws of quantum mechanics. This article explains what quantum gates are and why they must be unitary.
Do Quantum Gates Have to Be Unitary?
Yes, quantum gates must be unitary. Unitary operations are reversible, meaning that the goal of a quantum gate is to transform a quantum state without destroying or altering the information it contains. Unitary operations are also reversible, meaning that the original quantum state can be restored by reversing the application of the gate. As a result, unitary operations are essential for preserving the integrity of quantum information.
Unitary operations are also essential for creating quantum entanglement, a phenomenon in which two or more particles become linked together in a way that their quantum states can no longer be described independently. Unitary operations are the only way to create entanglement, as they allow for the manipulation of the quantum state in a way that is consistent with the laws of quantum mechanics. As such, they are the only operations that can create and maintain quantum entanglement.
What Are the Benefits of Using Unitary Operations?
Unitary operations are essential for preserving the integrity of quantum information. By preserving the quantum state, unitary operations allow for the manipulation of the quantum state without destroying or altering the information it contains. This allows for the creation of entanglement, a phenomenon in which two or more particles become linked together in a way that their quantum states can no longer be described independently.
In addition, unitary operations are essential for ensuring that the quantum information is accurate and reliable. Unitary operations are reversible, meaning that the original quantum state can be restored by reversing the application of the gate. As a result, they are the only operations that can guarantee that the quantum information is accurate and reliable.
How Are Unitary Operations Used in Quantum Computing?
Unitary operations are used in quantum computing to manipulate quantum information in a way that is consistent with the laws of quantum mechanics. Unitary operations are reversible, meaning that the original quantum state can be restored by reversing the application of the gate. This allows for the manipulation of the quantum state without destroying or altering the information it contains.
In addition, unitary operations are essential for creating quantum entanglement, a phenomenon in which two or more particles become linked together in a way that their quantum states can no longer be described independently. Unitary operations are the only way to create entanglement, as they allow for the manipulation of the quantum state in a way that is consistent with the laws of quantum mechanics. As such, they are the only operations that can create and maintain quantum entanglement.
Are There Any Limitations to Using Unitary Operations?
Yes, there are certain limitations to using unitary operations. Unitary operations are reversible, meaning that the original quantum state can be restored by reversing the application of the gate. However, this means that the quantum state can only be manipulated in a limited number of ways. Additionally, unitary operations are limited by the number of qubits that are available for manipulation, as each qubit can only be manipulated in a limited number of ways.
Furthermore, unitary operations are limited by the amount of time available for computation. Unitary operations require a significant amount of time for computation, as they require the manipulation of the quantum state in a way that is consistent with the laws of quantum mechanics. As such, the time available for computation must be considered when using unitary operations.
Are Unitary Operations Necessary for Quantum Computing?
Yes, unitary operations are necessary for quantum computing. Unitary operations are essential for preserving the integrity of quantum information, as they allow for the manipulation of the quantum state without destroying or altering the information it contains. In addition, unitary operations are essential for creating quantum entanglement, a phenomenon in which two or more particles become linked together in a way that their quantum states can no longer be described independently. As such, unitary operations are essential for the successful manipulation of quantum information.
How Can I Convert a Unitary Matrix to a set of One & Two Qubit Gates? 1 Minute Qiskit
In conclusion, the concept of quantum gates and their functionality in quantum computing is a fascinating topic that continues to captivate researchers and enthusiasts alike. While there is a lot that still needs to be explored and understood about the quantum world, it is clear that unitarity plays a crucial role in the functioning of quantum gates. By preserving the overall probabilities of quantum states, unitary gates ensure that quantum computations are accurate and reliable.
As quantum computing continues to evolve, it is likely that we will see new and innovative approaches to building quantum gates that can operate outside the constraints of unitarity. However, for the time being, the requirement for unitarity remains an essential component of quantum computing research and development. By understanding the principles underlying quantum gates and the importance of unitarity, we can begin to unlock the full potential of quantum computing and usher in a new era of technological progress.

