Paragraph 1:
As we dive deeper into the world of quantum mechanics, we come across a plethora of intriguing concepts that leave us spellbound. Amongst the many quantum numbers that govern the behavior of subatomic particles, the angular momentum quantum number stands out as a crucial factor in determining the characteristics of an atom. But have you ever wondered what exactly the angular momentum quantum number signifies? In this article, we will explore the significance of this quantum number and unravel the mysteries surrounding it.
Paragraph 2:
The angular momentum quantum number (l) is an integer that determines the shape of the electron’s orbital around the nucleus. It specifies the magnitude of the angular momentum of an electron in motion and can take any value from 0 to n-1, where n is the principal quantum number. The value of l helps to determine the energy, shape, and orientation of an atomic orbital. Understanding the angular momentum quantum number is crucial in comprehending the behavior of electrons and predicting chemical properties of elements. So, let’s delve deeper into the world of quantum mechanics and discover what the angular momentum quantum number has in store for us.
Angular Momentum Quantum Number
The angular momentum quantum number, also known as the orbital angular momentum quantum number, is an important quantum number in physics that describes the angular momentum of a particle. It is used to classify the energy levels of particles in an atom or molecule. It is one of the four quantum numbers that are used to describe the quantum state of a particle.
What is the Angular Momentum Quantum Number?
The angular momentum quantum number is a set of four numbers that describe the quantum state of a particle. These four quantum numbers are the principal quantum number (n), the angular momentum quantum number (l), the magnetic quantum number (m), and the spin quantum number (s). The angular momentum quantum number (l) is a number that describes the angular momentum of a particle.
The angular momentum quantum number is related to the orbital angular momentum of a particle which is the sum of the particle’s angular momentum with respect to the origin of the coordinate system. It is often represented by the letter l and can have values from 0 to n-1, where n is the principal quantum number. The angular momentum quantum number is closely related to the shape of the orbital, with different values corresponding to different orbital shapes.
What is the Significance of the Angular Momentum Quantum Number?
The angular momentum quantum number is an important quantum number in quantum mechanics and is used to describe the quantum state of a particle. It is one of the four quantum numbers that are used to describe the quantum state of a particle and is used to classify the energy levels of particles in an atom or molecule. It is used to determine the angular momentum of a particle, the orientation of its orbit, and the type of orbital it occupies.
The angular momentum quantum number is also important in determining the shape of the orbitals. Different values of the angular momentum quantum number correspond to different orbital shapes. For example, s-orbitals have an angular momentum quantum number of 0, p-orbitals have an angular momentum quantum number of 1, and so on. Thus, the angular momentum quantum number is an important tool in understanding the structure of atoms and molecules.
Frequently Asked Questions
This page provides information about the angular momentum quantum number. It answers questions related to the characteristics given by the angular momentum quantum number and its implications.
What is the Angular Momentum Quantum Number?
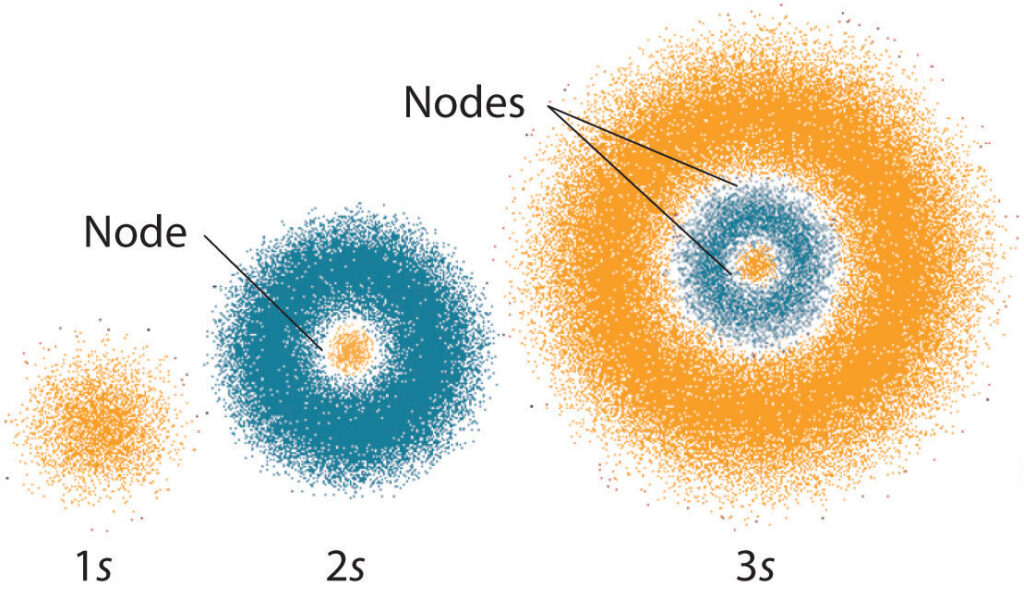
The angular momentum quantum number (l) is a quantum number that describes the shape of an electron orbital. It is also known as the orbital angular momentum quantum number, orbital quantum number, or azimuthal quantum number. This quantum number is related to the angular momentum of an electron in a particular atomic orbital. It determines the shape of the orbital and the number of angular nodes in the orbital. The angular momentum quantum number can have a value of 0, 1, 2, 3, and so on. The values of l increase as the orbital size and complexity increase.
What Characteristic is Given by the Angular Momentum Quantum Number?
The angular momentum quantum number is used to determine the shape of an electron orbital. It also determines the number of angular nodes in an orbital. These nodes are points in space where the value of the orbital wavefunction is zero. The angular momentum quantum number also determines the number of subshells in an orbital. Subshells are used to describe the energy levels of an electron in an orbital. The angular momentum quantum number also determines the magnetic quantum number, which is related to the orientation of an electron in an orbital.
What is the Relationship Between the Angular Momentum Quantum Number and the Magnetic Quantum Number?
The angular momentum quantum number and the magnetic quantum number are related because they both describe the orientation of an electron in an orbital. The angular momentum quantum number determines the magnetic quantum number, which is related to the orbital orientation of the electron. The magnetic quantum number (m) has values that range from -l to +l, where l is the angular momentum quantum number. This means that the magnetic quantum number can have a range of values that depend on the angular momentum quantum number.
What is the Relationship between the Angular Momentum Quantum Number and the Principal Quantum Number?
The angular momentum quantum number and the principal quantum number are related because they both describe the energy levels of an electron in an orbital. The principal quantum number (n) describes the energy levels of an electron in an orbital. The angular momentum quantum number determines the number of subshells in an orbital, which is related to the energy levels of the electron. The number of subshells increases as the angular momentum quantum number increases.
What are the Implications of the Angular Momentum Quantum Number?
The angular momentum quantum number has implications for the shape of an electron orbital and the energy levels of an electron in an orbital. It determines the number of angular nodes in an orbital, which are points in space where the value of the orbital wavefunction is zero. The angular momentum quantum number also determines the magnetic quantum number, which is related to the orientation of an electron in an orbital. The angular momentum quantum number also determines the number of subshells in an orbital, which is related to the energy levels of an electron.
Total Angular Momentum Quantum Number
In conclusion, the angular momentum quantum number is a crucial element in understanding the behavior of atomic particles. It characterizes the rotational motion of an electron around the nucleus and determines the shape and orientation of the electron’s orbit. By knowing the value of the angular momentum quantum number, we can predict the energy levels and spectral lines of an atom accurately. Additionally, the angular momentum quantum number is essential in determining the magnetic properties of atoms and molecules, which has significant implications for many fields, including chemistry, physics, and biology.
In summary, the angular momentum quantum number is a fundamental concept in the study of atomic structure and behavior. It provides crucial information about the shape, orientation, and energy levels of an atom, making it a crucial tool in understanding the workings of nature. As we continue to explore the mysteries of the universe, the angular momentum quantum number remains a vital piece of the puzzle, unlocking new discoveries and leading us to a deeper understanding of the world around us.