Quantum mechanics is a fascinating field of study that has revolutionized our understanding of the universe at the atomic and subatomic level. One of the most interesting aspects of quantum mechanics is the concept of orbitals, which are the regions of space around an atomic nucleus where electrons are most likely to be found. These orbitals have unique shapes and orientations, which are determined by a set of quantum numbers. In this article, we will explore one specific quantum number that plays a crucial role in describing the shape of an orbital.
The quantum number in question is known as the azimuthal quantum number, or l. This number describes the angular momentum of an electron in an orbital, which in turn determines the shape of the orbital. The value of l can range from 0 to n-1, where n is the principal quantum number. Each value of l corresponds to a specific shape of orbital, with l=0 representing an s orbital, l=1 representing a p orbital, l=2 representing a d orbital, and so on. Understanding the role of the azimuthal quantum number is essential to understanding the behavior of electrons in atoms and molecules, and is a key concept in the field of quantum mechanics.
The angular momentum quantum number (ℓ) describes the shape of the orbital. ℓ can take any integer value from 0 to (n-1), where n is the principal quantum number. Orbitals with ℓ = 0 are referred to as s-orbitals. Orbitals with ℓ = 1 are referred to as p-orbitals. Orbitals with ℓ = 2 are referred to as d-orbitals. Orbitals with ℓ = 3 are referred to as f-orbitals.
Which Quantum Number Describes the Shape of an Orbital?
Quantum numbers are a set of numbers that describe the state of an electron in an atom. The four quantum numbers are used to describe the position, spin, and energy of the electron. One of the quantum numbers, the angular momentum quantum number (l), is used to describe the shape of an electron orbital.
What is an Orbital?
An orbital is a region in space around an atom that describes the probability of finding an electron. These regions have different shapes, and the angular momentum quantum number (l) is used to describe the shape of the orbital. This quantum number can have values from 0 to n-1, where n is the principle quantum number.
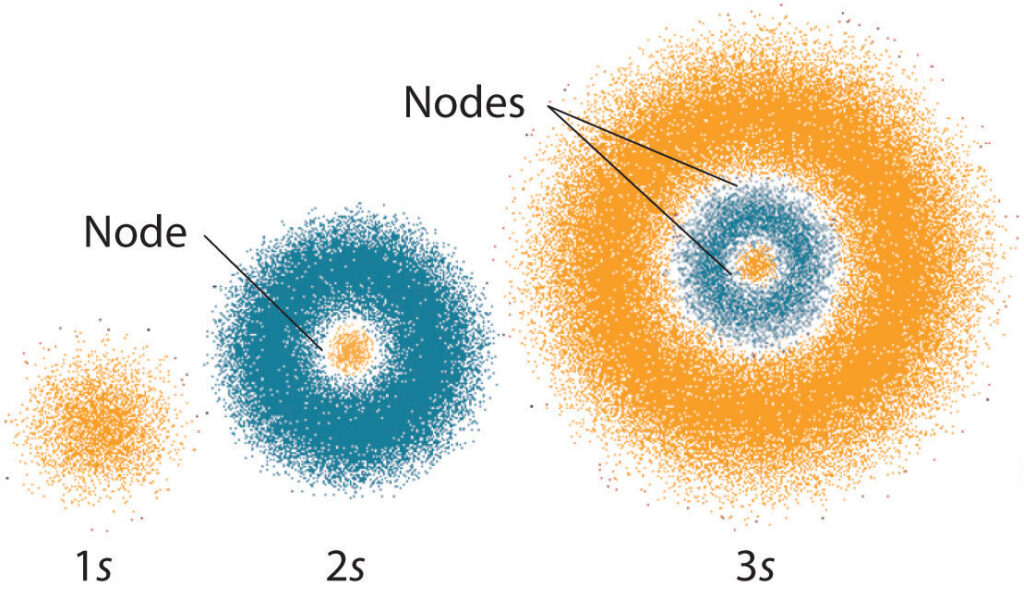
The s orbital is the simplest orbital, and it can contain up to two electrons. It is a spherical orbital with no nodes and has an l value of 0. The p orbital is slightly more complicated, and it can contain up to six electrons. It is shaped like a dumbbell with two lobes, and it has an l value of 1. The d orbital is even more complex, and it can contain up to ten electrons. It is shaped like a cloverleaf, and it has an l value of 2.
How Does the Angular Momentum Quantum Number Describe the Shape of an Orbital?
The angular momentum quantum number (l) is used to describe the shape of the orbital. The higher the value of l, the more complex the orbital shape. For example, an s orbital has an l value of 0, a p orbital has an l value of 1, and a d orbital has an l value of 2.
The angular momentum quantum number can also be used to determine the number of nodes in an orbital. A node is a region in an orbital where the probability of finding an electron is zero. An s orbital has no nodes, a p orbital has one node, and a d orbital has two nodes.
The angular momentum quantum number is an important tool for understanding the shapes of electron orbitals. It is used to describe the shape of the orbital and the number of nodes in the orbital. By understanding how this quantum number works, we can gain a better understanding of the structure of atoms.
Frequently Asked Questions
Here are the answers to some commonly asked questions about the quantum number that describes the shape of an orbital.
What is a quantum number?
A quantum number is a mathematical description of the state of a quantum system. It describes the energy, angular momentum, and other properties of the system. In the context of chemistry, quantum numbers are used to describe the characteristics of an atom or molecule, such as its energy levels, electron configuration, and the shape of its orbitals.
What is the quantum number that describes the shape of an orbital?
The quantum number that describes the shape of an orbital is called the angular momentum quantum number, or l. This quantum number is related to the angular momentum of the electron in the orbital and describes the shape of the orbital. It can take on values of 0, 1, 2, and so on, up to a maximum of n-1, where n is the principal quantum number.
What is an orbital?
An orbital is a region of space around an atom or molecule where an electron is likely to be found. Orbitals are defined by their shape, which is determined by the quantum numbers of the electron. Each orbital has a unique set of quantum numbers that describes its shape, size, and energy.
What is the maximum value of the angular momentum quantum number?
The maximum value of the angular momentum quantum number (l) is n-1, where n is the principal quantum number. This means that the maximum value of l for a given electron is determined by its principal quantum number. For example, if the principal quantum number is 3, then the maximum value of l is 2.
How is the angular momentum quantum number related to the shape of an orbital?
The angular momentum quantum number (l) is closely related to the shape of an orbital. As the value of l increases, the orbital becomes more complex in shape. The lowest value of l (0) describes an orbital that is spherical in shape, while higher values of l describe orbitals that are more distorted or elongated. The shape of the orbital is also affected by the other quantum numbers, such as the principal quantum number and the magnetic quantum number.

In conclusion, quantum numbers are an essential aspect of describing the properties of an atom. The shape of an orbital is described by the angular momentum quantum number, also known as the azimuthal quantum number. Understanding this quantum number is crucial in predicting the behavior of electrons in an atom and is a fundamental concept in the field of quantum mechanics.
As scientists continue to explore the properties of atoms and subatomic particles, the importance of quantum numbers will only become more evident. With the help of these numbers, physicists can predict the behavior of electrons with incredible accuracy, leading to new discoveries and advancements in technology. As such, a deeper understanding of quantum numbers, including the angular momentum quantum number, is essential for anyone interested in the field of physics or chemistry.